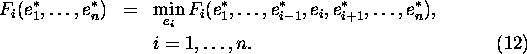These results extend easily on an arbitrary number of
actors. Suppose that there are n independent actors
(countries or regions), each of them releases
(
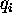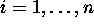) amount of CO
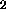per year into the atmosphere. The
total emission is equal to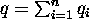 
. If each actor reduces
his own emission 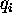to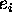 
then his expenditure will be
described by the utility function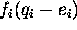 
which is a
monotonously decreasing function of its argument. All the
actors tend not only to realise the own ``egoistic''
interests,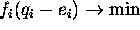 
, but also to the achievement of
the common ``altruistic'' aim,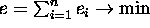 
. As we already did,
we introduce the coefficients of egoism,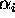 
, which make
these ``egoistic'' and ``altruistic'' criteria commensurable.
Using these coefficients we can fold these criteria into
one criterion
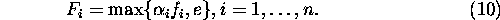
Therefore we got the following problem:
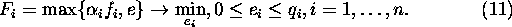
A solution of the problem is based on the analogous
equilibrium principle: the system will be at a stable and
efficient equilibrium, i.e. it will belong to the Pareto's
set, if such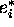 
exists that
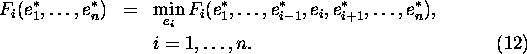
If we enumerate all actors, so that i < j if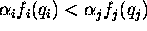 
, we save all the statements which have been
proven for the case of two actors, since all the proofs
are literally repeated. Therefore we omit these proofs
and formulate the final results.
In order to assure that the values 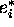describe the Pareto
equilibrium the existence
of such number m that ,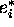 
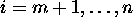are a solution of the
following equations:
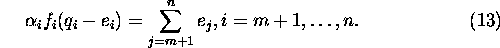
and that the functions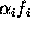 
and the values 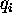for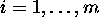 
satisfy the
inequalities
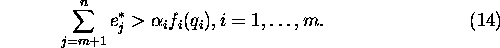
are a necessary and sufficient conditions.
Note that the equations (13) have one unique solution.
It is obvious that the number m separates the set of actors on two subsets: the first subset (with the numbers from 1 to m) is a community of super-altruists who reduce their emissions to zero, not depending on the behaviour of members of the second egoistic community (with the numbers from m+1 to n). In turn, the members of the egoistic community play their own game, not taking into consideration members of the first community. Note that the separation on the two communities can be done only a posteriori after the solution of (13) for different m is obtained and after the consequent test of the inequalities (14).
Certainly, the reality is more complex than our theory, and the existence of such sort of altruistic community is rather a theoretical abstraction than a real fact. Therefore, further on we shall consider the case when all the actors participate in the emissions game.