Nordhaus and Leimbach suggested the following form for R:
and the equations (13) are written in the form (for m = 0):
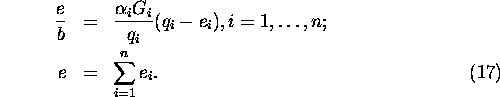
Let us suppose that all
where
Let us introduce new variables: the relative reduction of emission
Substituting
Let us consider one partial case when the functions
![]() have been estimated. In accordance to Nordhaus[5] and
Leimbach's[6] econometric estimation, the relative loss
of the Gross Domestic Product (GDP) for the i-th country,
(which are connected with the expenditures on CO
have been estimated. In accordance to Nordhaus[5] and
Leimbach's[6] econometric estimation, the relative loss
of the Gross Domestic Product (GDP) for the i-th country,
(which are connected with the expenditures on CO![]() reduction) depends only on the relative reduction of
emission
reduction) depends only on the relative reduction of
emission ![]() , so that
, so that
![]()
Nordhaus and Leimbach suggested the following form for
R: ![]() . Later on Leimbach[6] suggested using
the linear form
. Later on Leimbach[6] suggested using
the linear form ![]() . Unfortunately,
. Unfortunately, ![]() for both forms, but this is an artefact of regression
analysis used in econometrics. Further on we shall use a
``pure'' linear form where the coefficient b has some
intermediate value (for instance, b = 0.1). (We think
that we do not commit any great crime in respect to
econometrics). Then
for both forms, but this is an artefact of regression
analysis used in econometrics. Further on we shall use a
``pure'' linear form where the coefficient b has some
intermediate value (for instance, b = 0.1). (We think
that we do not commit any great crime in respect to
econometrics). Then
![]()
and the equations (13) are written in the form (for m =
0):
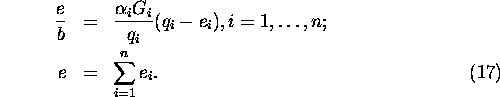
Let us suppose that all ![]() are known, i.e. all the
actors (countries) can be ranked along the axis ``altruism
- egoism''. Then the solution of (17) can be represented
as
are known, i.e. all the
actors (countries) can be ranked along the axis ``altruism
- egoism''. Then the solution of (17) can be represented
as
![]()
where
![]()
Let us introduce new variables: the relative reduction of
emission ![]() for the i-th actor, the relative
contribution of the i-th actor,
for the i-th actor, the relative
contribution of the i-th actor, ![]() , to the total
current emission. Then (18) can be re-written in a very
simple form:
, to the total
current emission. Then (18) can be re-written in a very
simple form:
![]()
Substituting ![]() from (20) to (19) we get
from (20) to (19) we get
![]()