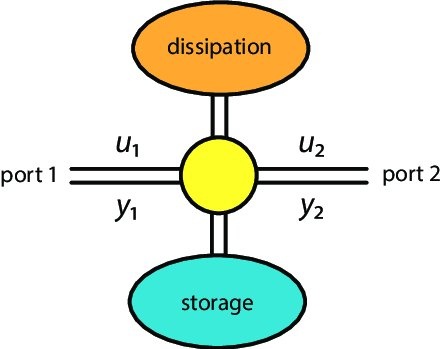
Port-Hamiltonian systems provide a unified and natural modeling framework for energy based modeling of large classes of real world physical systems. This workshop aims at introducing basic concepts in port-Hamiltonian modeling of power grids, discussing recent advances and addressing open questions. The main topics are
- Physical interpretability: How are external inputs to the energy converting system modeled, i.e. the side that is not connected to the power grid? How are surrogate models interconnected if their mathematical structure is port-Hamiltonian but the supply rate has the wrong physical dimensions?
- Stability: How to assess the stability of the desired state in a multi-stable system? Which measures can distinguish between different Lyapunov functions or representations of the same physical system? How can the freedom of representation be put to use? Which difficulties arise when the system is pumped with energy and what solutions are there?
- Robustness: How can the most robust representation be sorted out on theoretical grounds or be extracted from data?
Location
Technische Universität Berlin
Institute for Mathematics
Straße des 17. Juni 136, 10587 Berlin
room: MA 376 (west wing)
The coffee break takes place in room 464.
Schedule
Date: 8. April, 10 AM - 6 PM
- 10:00 - 10:55 | Volker Mehrmann | Energy based modeling of energy networks, an introduction
- 11:00 - 11:30 | Juan Machado and Johannes Schiffer | On shifted passivity and stabilization in the application of port-Hamiltonian systems theory
- lunch break
- 12:30 - 13:00 | Hannes Gernandt | Port-Hamiltonian modeling and control design for electric vehicle charging stations
- 13:00 - 13:30 | Jakob Niehues | Normal form analysis of power systems
- coffee (room 464)
- optional: break-out sessions (open end)
Detailed Program
Volker Mehrmann | Energy based modeling of energy networks, an introduction
Most real world dynamical systems consist of subsystems from different physical domains, modelled by partial-differential equations, ordinary differential equations, and algebraic equations, combined with input and output connections. To deal with such complex systems, in recent years energy based modeling via the class of dissipative port-Hamiltonian (pH) descriptor systems has emerged as a very successful mathematical modeling methodology. The main reasons are that the network based interconnection of pH systems is again pH, Galerkin projection in PDE discretization and model reduction preserve the pH structure, and the physical properties are encoded in the geometric properties of the flow as well as the algebraic properties of the equations. Furthermore, dissipative pH systems form a very robust representation under structured perturbations and directly indicate Lyapunov functions for stability analysis. Another advantage of energy based modeling via pH systems is that each separate model of a physical system can be a whole model catalog from which models can be chosen in an adaptive way within simulation and optimization methods. We describe the model class of constrained pH systems and show how many classical real world mathematical models in energy systems can be formulated in this class.
Juan Machado and Johannes Schiffer | On shifted passivity and stabilization in the application of port-Hamiltonian systems theory
Many physical systems naturally admit a port-Hamiltonian representation. Most often the associated natural Hamiltonian is then centered at the trivial equilibrium, i.e., the origin. From a practical perspective, this trivial equilibrium is not an operating point of interest. Instead, one is interested in an equilibrium arising from applying a (constant) forcing term, e.g. a voltage or force, to the system. Thus, a key question is whether the system’s input-output map expressed relative to the forced, non-trivial equilibrium also admits a port-Hamiltonian structure with the associated passivity property. In this talk, we showcase that this is generally not the case and revisit existing conditions for shifted passivity as well as passivity-based control approaches for stabilization of pH systems.
Hannes Gernandt | Port-Hamiltonian Modelling and Control Design for electric vehicle charging stations
We generate a port-Hamiltonian (pH) model of an electric vehicle charging station. Here the battery of the vehicle is connected to an AC grid via transmission lines, converters, and filters. We use general averaged pH system models to approximate the switching behavior of the converters by introducing additional parameter states. More generally, the pH structure is then exploited for the design of stabilizing controllers of the system. Finally, we compare the different pH control approaches within a simulation model of a charging station.
Jakob Niehues | Normal form analysis of power systems
Future power grids will be dominated by grid-forming inverters, that have to provide inertia and stability without centralized rotating masses like synchronous generators. The normal form for grid-forming grid actors has recently been developed as a unified language for all sorts of grid actors. For the first time, it is possible to analyze the stability of today's and future power grids in a general, technology neutral way. The normal form is derived from symmetry considerations applied to the basic functionality of power grid dynamics. Port-Hamiltonian modeling can be seen as a complementary approach, aggregating the fundamental building blocks of the system. In this talk, we introduce the concept of normal form analysis and outline possible connections to the port-Hamiltonian formulation of power grids.
Optional break-out sessions
We discuss the key questions mentioned in the workshop's abstract (above) and the connection between normal form and port-Hamiltonian modeling.