
Technical Policy Briefing Notes - 2
Cost-Effectiveness Analysis
Description of the Method
Policy Briefs
Cost-Effectiveness Analysis
Description of the Method
Cost-Effectiveness Analysis (CEA) is a widely used decision
support tool. It compares alternative options for achieving similar
outputs (or objectives). In this regard it is a relative measure,
providing comparative information between choices. It has been widely
used in environmental policy analysis, because it avoids monetary
valuation of benefits, and instead quantifies benefits in physical
terms.
At the technical or project level, CEA can be used to compare and rank alternative options. It does this by assessing options in terms of the cost per unit of benefit delivered, e.g. cost per tonne of pollution abated. This identifies those options that deliver highest benefit for lowest cost (i.e. the most cost-effective). As well as ranking different options, such an analysis can be used for benchmarking, see box.
At the project, policy or programme level, where combinations of options are needed, CEA can be used to assess the most cost-effective order of options, and so identify the least-cost path for achieving pre-defined policy targets. This is undertaken through the use of marginal abatement cost (MAC) curves. The approach can also identify the largest benefits possible with the available resources, and can even be used to help set targets, by selecting the point where cost-effectiveness falls significantly (i.e. where there are disproportionately high costs for low benefits).
Cost-effectiveness analysis has been widely used in European and Member State policy appraisal, and was previously the main approach used for air quality policy (Watkiss et al, 2007). Air quality concentration or deposition target levels were set on a scientific basis, and the costs of alternative ways of achieving these targets (or progressing towards them) were assessed using CEA.
It has also been used in risk-based flood protection assessment, particularly for coastal zones (e.g. RIVM, 2004) assessing the costeffectiveness of achieving flood protection targets (defined as a level of acceptable risk, such as protection against a 1 in 10000 year return period).
Most recently, cost-effectiveness analysis has become the main appraisal technique used for climate change mitigation, as it allows the comparison and ranking of greenhouse gas (GHG) abatement options, using the costeffectiveness metric of cost per tonne of GHG abated (€/tCO2). There has also been widespread use of marginal abatement cost curves for mitigation. These show the relative ranking of options in order of cost-effectiveness, and can be used for identifying the least cost way of achieving emission reductions including cross-economy targets (e.g. CCC, 2008).
Because of the widespread use of CEA for climate change mitigation, many commentators have also highlighted its potential use for climate change adaptation. However, the application of CEA to adaptation involves a number of major differences, see Box 2.
Cost-effectiveness analysis involves a series of common methodological steps.
This information can then be used as an input to form a marginal abatement cost curve. Cost curves have been used for many decades in policy (and mitigation) analysis. In graphical terms, they are often presented as cumulative bar charts.
In simple terms, a cost curve presents all options in order of unit cost-effectiveness analysis, starting with the most cost-effective. At the same time, it also assesses the total cumulative effectiveness of each option, as it is added. When considered together, this allows the estimation of the least-cost way to achieve a plan, programme or policy target /objective.
An example is included below, showing a typical mitigation cost curve. Each bar represents a specific option. The options are arranged in order of cost-effectiveness (left to right), as measured on the vertical axis by the cost per unit of abatement – €/CO2. The width of each bar indicates the total abatement potential of each option (i.e. the total effectiveness, in tonnes of CO2) – noting this could be for a local plan or a national level analysis. Wider bars show options that can achieve larger total benefits, i.e. which reduce more emissions. In the example, the marginal abatement costs of some cost-effective options are negative, showing these achieve benefits at negative cost, so called no regret options (e.g. energy efficiency).
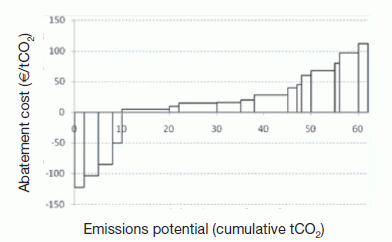
Example cost curve.
At the technical or project level, CEA can be used to compare and rank alternative options. It does this by assessing options in terms of the cost per unit of benefit delivered, e.g. cost per tonne of pollution abated. This identifies those options that deliver highest benefit for lowest cost (i.e. the most cost-effective). As well as ranking different options, such an analysis can be used for benchmarking, see box.
At the project, policy or programme level, where combinations of options are needed, CEA can be used to assess the most cost-effective order of options, and so identify the least-cost path for achieving pre-defined policy targets. This is undertaken through the use of marginal abatement cost (MAC) curves. The approach can also identify the largest benefits possible with the available resources, and can even be used to help set targets, by selecting the point where cost-effectiveness falls significantly (i.e. where there are disproportionately high costs for low benefits).
Box 1. Benchmarking using CEA
Cost-effectiveness analysis can be used to benchmark options, i.e. by setting thresholds. This approach is often used in considering new treatments in health service provision (e.g. in the UK), where the clinic effectiveness of new interventions are compared against a cost-effectiveness threshold, measured as the cost (£) per Quality Adjusted Life Year (QALY). New treatments or drugs are considered cost-effective if they are lower than £20 000 to £30 000 per QALY (NICE, 2010). Such an approach is needed because publicly funded healthcare systems cannot pay for every new medical treatment that becomes available. As there are limited resources, choices have to be made, cost-effectiveness analysis helps provide the largest benefits with the available resources.
Cost-effectiveness analysis can be used to benchmark options, i.e. by setting thresholds. This approach is often used in considering new treatments in health service provision (e.g. in the UK), where the clinic effectiveness of new interventions are compared against a cost-effectiveness threshold, measured as the cost (£) per Quality Adjusted Life Year (QALY). New treatments or drugs are considered cost-effective if they are lower than £20 000 to £30 000 per QALY (NICE, 2010). Such an approach is needed because publicly funded healthcare systems cannot pay for every new medical treatment that becomes available. As there are limited resources, choices have to be made, cost-effectiveness analysis helps provide the largest benefits with the available resources.
Box 2. Comparing Mitigation and
Adaptation
Cost-effectiveness analysis has become the primary appraisal method for mitigation. However, adaptation is very different to mitigation, for the following reasons:
Mitigation involves a single, common metric for benefits, i.e. tonnes of GHG emissions. This metric relates to a global burden, so a reduction in a tonne of GHG emissions is treated the same, irrespective of the technology, sector or location. This means a tonne of CO2 abated from road transport in an urban area has the same benefit (and unit of effectiveness) as a tonne abated from the electricity sector in a rural location. This allows equivalent cross-economy analysis of options using €/tCO2.
In contrast, adaptation is a response to a local, regional or national level impact, rather than to a global burden, and involves different types of risks in different sectors. There is therefore no common single metric which allows cross-sectoral cost-effectiveness analysis. Furthermore, there are often many risks even within a single sector, which can make even sectoral CEA studies challenging: for example, adaptation to sea level rise (SLR) can involve protecting people from flood risk, reducing coastal erosion, conserving coastal ecosystems, etc. all of which involve different metrics. Finally, the analysis of impacts in adaptation (rather than burdens in mitigation) means that technology, location and time period are important: for adaptation, it makes a different how, where and when cost-effectiveness is assessed.
Cost-effectiveness analysis has become the primary appraisal method for mitigation. However, adaptation is very different to mitigation, for the following reasons:
Mitigation involves a single, common metric for benefits, i.e. tonnes of GHG emissions. This metric relates to a global burden, so a reduction in a tonne of GHG emissions is treated the same, irrespective of the technology, sector or location. This means a tonne of CO2 abated from road transport in an urban area has the same benefit (and unit of effectiveness) as a tonne abated from the electricity sector in a rural location. This allows equivalent cross-economy analysis of options using €/tCO2.
In contrast, adaptation is a response to a local, regional or national level impact, rather than to a global burden, and involves different types of risks in different sectors. There is therefore no common single metric which allows cross-sectoral cost-effectiveness analysis. Furthermore, there are often many risks even within a single sector, which can make even sectoral CEA studies challenging: for example, adaptation to sea level rise (SLR) can involve protecting people from flood risk, reducing coastal erosion, conserving coastal ecosystems, etc. all of which involve different metrics. Finally, the analysis of impacts in adaptation (rather than burdens in mitigation) means that technology, location and time period are important: for adaptation, it makes a different how, where and when cost-effectiveness is assessed.
Cost-effectiveness analysis has been widely used in European and Member State policy appraisal, and was previously the main approach used for air quality policy (Watkiss et al, 2007). Air quality concentration or deposition target levels were set on a scientific basis, and the costs of alternative ways of achieving these targets (or progressing towards them) were assessed using CEA.
It has also been used in risk-based flood protection assessment, particularly for coastal zones (e.g. RIVM, 2004) assessing the costeffectiveness of achieving flood protection targets (defined as a level of acceptable risk, such as protection against a 1 in 10000 year return period).
Most recently, cost-effectiveness analysis has become the main appraisal technique used for climate change mitigation, as it allows the comparison and ranking of greenhouse gas (GHG) abatement options, using the costeffectiveness metric of cost per tonne of GHG abated (€/tCO2). There has also been widespread use of marginal abatement cost curves for mitigation. These show the relative ranking of options in order of cost-effectiveness, and can be used for identifying the least cost way of achieving emission reductions including cross-economy targets (e.g. CCC, 2008).
Because of the widespread use of CEA for climate change mitigation, many commentators have also highlighted its potential use for climate change adaptation. However, the application of CEA to adaptation involves a number of major differences, see Box 2.
Cost-effectiveness analysis involves a series of common methodological steps.
- Establish the effectiveness criteria.
- Collate a list of options.
- Collect cost data for each option – noting this involves the full costs over the lifetime of the option, including capital and operating costs – and thus requires all values to be expressed on a common economic basis (in equivalent terms using discount rates and either an equivalent annualised cost or a total present value).
- Assess the potential benefits (effectiveness) of each option. In many but not all, these are expressed as an annual benefit, relative to a baseline or reference case.
- Combine these to estimate the costeffectiveness, by dividing the lifetime cost by the lifetime benefit (or annualised costs by annualised benefit).
This information can then be used as an input to form a marginal abatement cost curve. Cost curves have been used for many decades in policy (and mitigation) analysis. In graphical terms, they are often presented as cumulative bar charts.
In simple terms, a cost curve presents all options in order of unit cost-effectiveness analysis, starting with the most cost-effective. At the same time, it also assesses the total cumulative effectiveness of each option, as it is added. When considered together, this allows the estimation of the least-cost way to achieve a plan, programme or policy target /objective.
An example is included below, showing a typical mitigation cost curve. Each bar represents a specific option. The options are arranged in order of cost-effectiveness (left to right), as measured on the vertical axis by the cost per unit of abatement – €/CO2. The width of each bar indicates the total abatement potential of each option (i.e. the total effectiveness, in tonnes of CO2) – noting this could be for a local plan or a national level analysis. Wider bars show options that can achieve larger total benefits, i.e. which reduce more emissions. In the example, the marginal abatement costs of some cost-effective options are negative, showing these achieve benefits at negative cost, so called no regret options (e.g. energy efficiency).

Example cost curve.
To undertake a policy CEA, a
target level of total effectiveness is first set and the cost curve is
generated. As the graph presents options in order of
cost-effectiveness, it estimates the cumulative least-cost pathway to
achieve the target, because it implements those options that have high
benefits for low cost first. By contrast, if the least cost-effective
options were implemented first (those on the right of the figure), it
would cost far more to achieve the same target level.
The combination of options needed to achieve the target can thus be read off the graph. A similar approach can be used to derive the total costs of different levels of ambition. In practice, CEA is more involved, and further checks are needed to ensure that options can be implemented together, and to consider other criteria.
The combination of options needed to achieve the target can thus be read off the graph. A similar approach can be used to derive the total costs of different levels of ambition. In practice, CEA is more involved, and further checks are needed to ensure that options can be implemented together, and to consider other criteria.
 download this briefing note
download this briefing note