Fig. 4 demonstrates how the global mean temperature ![]() evolves with
the modification of S'. Note that a moderate mutation rate (r=0.01, Curve b)
significantly extends the homeostatic effect as compared to the case without
mutation (Curve a).
evolves with
the modification of S'. Note that a moderate mutation rate (r=0.01, Curve b)
significantly extends the homeostatic effect as compared to the case without
mutation (Curve a).
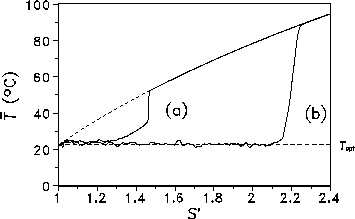
Figure 4: Global mean temperature ![]() vs. insolation S' for r=0 (a) and r=0.01 (b). The curved dashed line indicates the planetary temperature without life.
vs. insolation S' for r=0 (a) and r=0.01 (b). The curved dashed line indicates the planetary temperature without life.
Our general finding is that the extended model is an even better self-regulator than the simple LWM. The wiggles around the optimal control line
![]() are finite-size effects which will disappear on an infinite
lattice. As mentioned above, however, the dependence of self-stabilizing behaviour
on mutation is quite massive: for r=0 the critical insolation for vegetation
breakdown is given by
are finite-size effects which will disappear on an infinite
lattice. As mentioned above, however, the dependence of self-stabilizing behaviour
on mutation is quite massive: for r=0 the critical insolation for vegetation
breakdown is given by ![]() , while for r=0.01 the critical value
has increased to 2.19!
, while for r=0.01 the critical value
has increased to 2.19!
We generalize these observations by calculating ![]() as a function of r. The result is shown in Fig. 5, which clearly reveals the existence of an
optimum mutation rate
as a function of r. The result is shown in Fig. 5, which clearly reveals the existence of an
optimum mutation rate ![]() . The associated maximum critical
insolation strength is given by
. The associated maximum critical
insolation strength is given by ![]() .
.
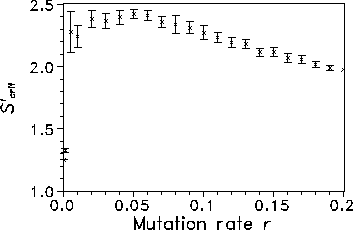
Figure 5: Upper-limit insolation ![]() for biosphere
homeostasis as a function of mutation rate r. All values result from averaging
over 10 different simulations; the error bars are included.
for biosphere
homeostasis as a function of mutation rate r. All values result from averaging
over 10 different simulations; the error bars are included.
The different realizations A and B (see Eqs. 10 and 11) for the CA growth rules result in rather distinct responses to increasing insolation. This is demonstrated in Fig. 6, which contrasts the evolution of ![]() with growing S' and identical r=0.05 for the two versions. We observe
that the critical insolation in case A is significantly smaller than in case B.
with growing S' and identical r=0.05 for the two versions. We observe
that the critical insolation in case A is significantly smaller than in case B.
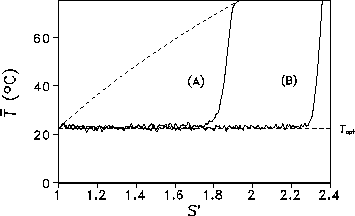
Figure 6: Global mean temperature ![]() vs. insolation S' for version A and B, respectively, of the CA growth rules (mutation rate r=0.05).
vs. insolation S' for version A and B, respectively, of the CA growth rules (mutation rate r=0.05).
Of course, the increase of S' heavily influences the species spectrum which
adjusts in a self-stabilizing way. As a matter of fact, the rms-deviation ![]() significantly decreases when the sun becomes brighter (or the greenhouse
gases accumulate). In other words, adaptation to non-optimal environmental
conditions implies loss of biodiversity. Fig. 7 depicts the species spectra
associated with two different values of S' and identical mutation rate.
significantly decreases when the sun becomes brighter (or the greenhouse
gases accumulate). In other words, adaptation to non-optimal environmental
conditions implies loss of biodiversity. Fig. 7 depicts the species spectra
associated with two different values of S' and identical mutation rate.
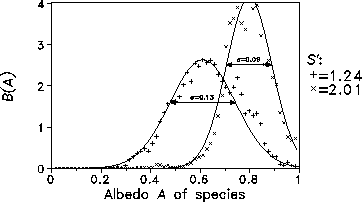
Figure 7: Species spectra for S'=1.24 and 2.01, respectively. r=0.01.
The dwindling of biodiversity can be explained analytically, if we inspect the
behaviour of ![]() as a function of
as a function of ![]() . Local energy balance implies
. Local energy balance implies
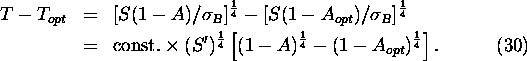
Linearization of the term in square brackets yields
![]()
in the neighbourhood of optimum albedo ![]() which is itself a strictly increasing function of the insolation S. From the latter equation it becomes clear that
a fixed deviation
which is itself a strictly increasing function of the insolation S. From the latter equation it becomes clear that
a fixed deviation ![]() from the optimal albedo, i.e.,
from the optimal albedo, i.e.,
![]() , is punished the more severely the larger S' grows:
, is punished the more severely the larger S' grows:
![]() increases monotonically with S' and the growth probability
increases monotonically with S' and the growth probability
![]() is a unimodular function with unique maximum at
is a unimodular function with unique maximum at ![]() . So for
higher S'>1, species have to possess a closer-to-optimum albedo in order to
exhibit comparable fitness. As a consequence, the spectrum becomes steeper
and steeper with growing insolation.
. So for
higher S'>1, species have to possess a closer-to-optimum albedo in order to
exhibit comparable fitness. As a consequence, the spectrum becomes steeper
and steeper with growing insolation.