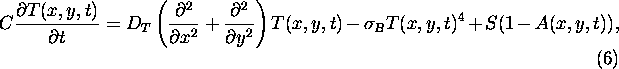
where
The ``climate'' here coincides with the temperature field T(x,y,t), which is
governed by an elementary energy balance equation (see, e.g.,
Henderson-Sellers and McGuffie 1990):
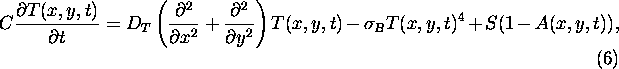
where ![]() denotes the diffusion constant and A(x,y,t) represents the
spatiotemporal distribution of albedo. The latter reflects the prevailing
vegetation pattern. The homogeneous solutions of Eq. 6 are equivalent
to the solutions of Eq. 1 of the original LWM.
denotes the diffusion constant and A(x,y,t) represents the
spatiotemporal distribution of albedo. The latter reflects the prevailing
vegetation pattern. The homogeneous solutions of Eq. 6 are equivalent
to the solutions of Eq. 1 of the original LWM.
We consider an extended biosphere consisting of infinitely many different
species, which may be conveniently classified by their specific albedos
![]() . So the variable A serves a twofold purpose, namely
(i) to label the ``daisies'' stored in the genetic pool, and
(ii) to express their radiative properties. As a consequence, the vegetation
dynamics within our model can be directly represented by the albedo dynamics.
. So the variable A serves a twofold purpose, namely
(i) to label the ``daisies'' stored in the genetic pool, and
(ii) to express their radiative properties. As a consequence, the vegetation
dynamics within our model can be directly represented by the albedo dynamics.
To achieve this we have to translate the vegetation growth rules, which can be set up in the spirit of the LWM, into albedo modification rules. Their dependence on T and Eq. 6 then determine the coevolution of albedo and temperature field in the plane. As the analytic solution of this intricate non-linear dynamics is unfeasible, we will have to resort to numerical computation schemes based on discretization of the system. It is therefore reasonable to employ the CA approach from the outset [17, 18]. One major advantage of this approach is the fact that consistent albedo modification rules can be written down immediately.
The CA is constructed as follows: the plane is replaced by a quadratic lattice
![]() , where
, where ![]() and
the basic spatial units
and
the basic spatial units ![]() ,
, ![]() can be chosen arbitrarily. Time
proceeds in discrete steps
can be chosen arbitrarily. Time
proceeds in discrete steps ![]() , where
, where ![]() and
and
![]() is again an optional unit. Thus any systems variable F becomes
a function
is again an optional unit. Thus any systems variable F becomes
a function ![]() .
.
The occurrence of vegetation in a particular cell ![]() at time
at time ![]() can be indicated
by a binary coverage function
can be indicated
by a binary coverage function ![]() .
The albedo dynamics is then determined by the following rules:
.
The albedo dynamics is then determined by the following rules:
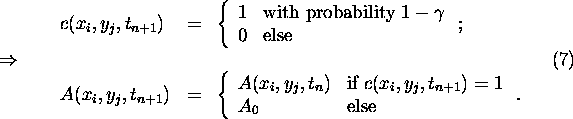
Then choose at random a next-neighbour cell ![]() of
of ![]() and make the following distinction:
and make the following distinction:
So in the first version, (A), the growth rate depends on the state of the area that will be covered by the vegetation in the next time step, while in the second version, (B), the temperature of the vegetation patch which initiates the growth determines the growth probability. It turns out that this innocent-looking local distinction induces rather different behaviour even at the systems scale (see below).
The function f in (9) offers the opportunity to incorporate also more
sophisticated biological effects: by choosing, for instance,
![]()
where R is a random number distribution with the properties
![]()
it is possible to take mutations of the albedo into account. Here ![]() can be
interpreted as the mutation rate.
can be
interpreted as the mutation rate.
The CA is completed by solving the temperature evolution equation (6) by an explicit finite-difference scheme on the square lattice with the same resolution as employed for the growth dynamics. The discretization step must be chosen in the way that the stability of the explicit scheme is guaranteed and no bifurcation (as, e.g., in the logistic map) takes place. A list of the chosen parameter settings is shown in Table 1. These values are used unless stated otherwise.
| Parameter | Value |
| | |
|
| 500 |
| C | 2500 |
|
| 0.5 |
|
| 0.02 |
|
| 1 |
|
| 1 |
|
| 1 |
Comparison with the original model
Our extended geophysiological model for biosphere-geosphere
interactions contains all the dynamics of the zero-dimensional LWM as a
special subprocess. To demonstrate this we have to consider the true evolution
of the vegetation density N. Within the discrete CA
formalism, N is defined as follows:
![]()
where ![]() denotes an averaging over a statistical ensemble.
Thus
denotes an averaging over a statistical ensemble.
Thus ![]() represents the probability of encountering vegetation
of any type in cell
represents the probability of encountering vegetation
of any type in cell ![]() at time
at time ![]() . The dynamics of N is implicitly
determined by the rules summarized in Eqs. 7 to 9.
. The dynamics of N is implicitly
determined by the rules summarized in Eqs. 7 to 9.
To simplify the calculations we restrict the vegetation to one species in two
spatial dimensions without considering mutations (f(A)=A). We have
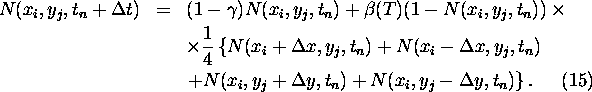
The next step is to take the continuous limit by making a Taylor expansion
in ![]() ,
, ![]() , and
, and
![]() up to second order in space and first order in time, which results
in the following expressions:
up to second order in space and first order in time, which results
in the following expressions:
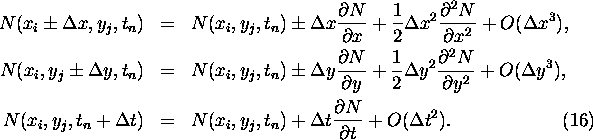
Substituting the approximations in Eq. 15 and performing some
transformations, the following PDE can be obtained for growth version A, if we
neglect the terms of higher order:
![]()
where ![]() ,
, ![]() ,
, ![]() , and
, and ![]() .
In order to have a non-vanishing diffusion for low values of
.
In order to have a non-vanishing diffusion for low values of ![]() ,
, ![]() ,
, ![]() must be enlarged. This can be compensated by a lower value of
must be enlarged. This can be compensated by a lower value of ![]() , which ensures also the stability of the discretization scheme.
, which ensures also the stability of the discretization scheme.
For growth version B the density N is determined by
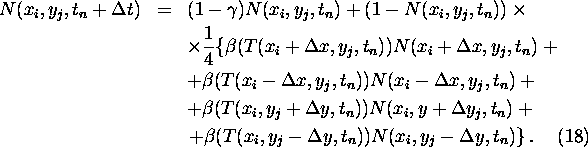
The resulting PDE for N is
![]()
Let us emphasize here that for homogeneous solutions, i.e.,
![]() , the equations (15) and (18), respectively, are
identical to the zero-dimensional LWM for one species (see Eq. 3).
, the equations (15) and (18), respectively, are
identical to the zero-dimensional LWM for one species (see Eq. 3).
If we include mutations of the albedo according to (12) for the
homogeneous solution N(A;t) we get:
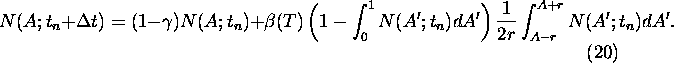
Taylor expansion in A yields the following expression for ![]() :
:
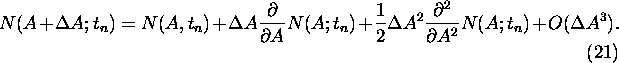
Inserting (21) into (20) and taking the continuous limit in t, the following equation, valid for small mutation rates r, is obtained:
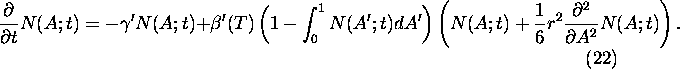
This analysis can be expanded to all aspects of our full CA to demonstrate
that the discretization preserves the right physics and biology.