The proposed model is called the ``simplest'' model because it contains the minimal set
of state variables to realize a global vegetation model incorporating the global carbon cycle.
The climate of our hypothetical planet is described by one variable, namely,
the annual average temperature of its surface. The planetary atmosphere
is an isotropic one, containing one ``greenhouse'' gas - 
- ,with
carbon concentration C(t). The equation for temperature will be [3, 8]:
where k is the surface heat capacity, S is the solar radiation, 
is the surface albedo, and 
is the Stephan-Boltzmann constant. The ``greenhouse''
effect is described by the function 
, which is a monotonous decreasing
function with saturation for 
: 
, 
. A good approximation is a hyperbola.
We consider the ``point'' planet to be without ocean, covered by vegetation with the
density 
(in carbon units per unit surface). If 
is the total
area of the planet, then 
is the total amount of carbon contained
in the vegetation. (Without loss of generality we can put 
).
As in the previous model we assume that the albedo depends on the
density of vegetation N, so that is a monotonous decreasing
function of N (see Fig. 1).
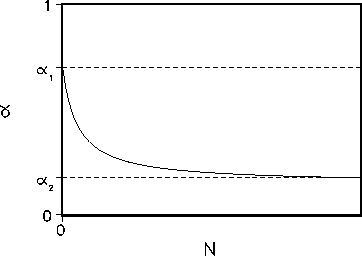
Figure 1: Albedo as a function of the carbon mass in the vegetation N.
We include in the model the simplest two-compartmental submodel of the global carbon cycle, when the total carbon is allocated to the compartments: atmosphere and biota (vegetation), with corresponding concentrations C and N.
The equation for biota is:
where P is the annual net-production of vegetation, m is the value which
is inverse to the residence time of carbon in the biota, 
.
The equation for atmospheric carbon is
where e(t) is the annual anthropogenic emission.
The total amount of carbon A(t)=C(t)+N(t) has the following evolution in time:
and integrating the equation one obtains
where 
.
Using the equality to exclude the variable C(t) from the equations
(2) and (3), we get
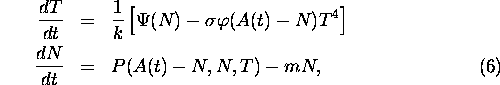
where
The system is the simplest model of the biosphere of our hypothetical planet.
Due to the explicit time dependence of A(t) it is a non-autonomous dynamical
system. If we suppose that A(t) changes quasi-stationarily with t, i.e. is
a slow process in relation to T and N then
Therefore we analyse the stationary solutions of the system with 
.
and 