First, we test the decay of self-stabilizing power with increasing patchiness in the 2D Daisyworld without animals.
Fig. 2 summarizes our findings regarding the relation between global mean
temperature ![]() and the percolation parameter
and the percolation parameter ![]() . It can be observed that even
the fragmented biosphere is able to stabilize the planetary temperature near
the optimal value, unless p exceeds a value of approximately 0.4.
. It can be observed that even
the fragmented biosphere is able to stabilize the planetary temperature near
the optimal value, unless p exceeds a value of approximately 0.4.
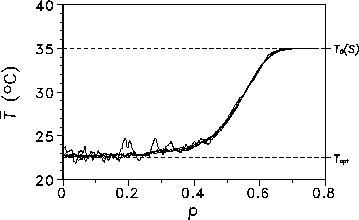
Figure: Convergence of numerical results for p-![]() -relationship
for increasing lattice size ranging from
-relationship
for increasing lattice size ranging from ![]() (wiggliest line) to
(wiggliest line) to
![]() (smoothest line).
S has been fixed to a value that
generates a geophysical planetary temperature
(smoothest line).
S has been fixed to a value that
generates a geophysical planetary temperature ![]() .
.
The numerical results are robust. As a matter of fact, Fig. 2 shows for a series of extensive
calculations with
increasing lattice dimensions that finite-size effects can be neglected.
It actually turns out that the above-mentioned threshold value
for patchiness has universal character. The adaptive power of Daisyworld
clearly breaks down when p approaches the value ![]() .
.
The explanation for this phenomenon is simple but illuminating: for ![]() the growth space has lost its connectivity and is broken up into many isolated
domains. Our toy model hence provides us with clear-cut evidence that the
ecological performance of a system directly depends on its connectivity!
For detailed results concerning, for example, the corresponding change in the species spectrum see again von Bloh[5].
the growth space has lost its connectivity and is broken up into many isolated
domains. Our toy model hence provides us with clear-cut evidence that the
ecological performance of a system directly depends on its connectivity!
For detailed results concerning, for example, the corresponding change in the species spectrum see again von Bloh[5].