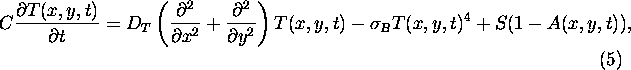
where
In general, the stable coexistence of many different species in Daisyworld can be brought about either by temporal fluctuations or by extending the spatial dimensionality. In this paper, the second approach is used and our planet will be represented by a 2D plane with coordinates x and y [11, 5].
The ``climate'' here coincides with the temperature field T(x,y,t), which is
governed by an elementary energy balance equation (see, e.g.,
[12]):
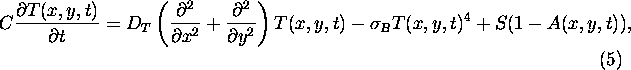
where ![]() denotes the diffusion constant and A(x,y,t) represents the
spatiotemporal distribution of albedo. The latter reflects the prevailing
vegetation pattern.
denotes the diffusion constant and A(x,y,t) represents the
spatiotemporal distribution of albedo. The latter reflects the prevailing
vegetation pattern.
We consider an extended biosphere consisting of infinitely many different
species, which may be conveniently classified by their specific albedos
![]() . So the variable A serves a twofold purpose, namely
(i) to label the ``daisies'' stored in the genetic pool, and
(ii) to express their radiative properties. As a consequence, the vegetation
dynamics within our model can be directly represented by the albedo dynamics.
. So the variable A serves a twofold purpose, namely
(i) to label the ``daisies'' stored in the genetic pool, and
(ii) to express their radiative properties. As a consequence, the vegetation
dynamics within our model can be directly represented by the albedo dynamics.
To achieve this we have to translate the vegetation growth rules, which can be set up in the spirit of the LWM, into albedo modification rules. Their dependence on T and Eq. 5 then determine the coevolution of albedo and temperature field, respectively, in the plane. As the analytic solution of this intricate nonlinear dynamics is unfeasible, we will have to resort to numerical computation schemes based on discretization of the system. It is therefore reasonable to employ the CA approach from the outset [13, 14]. One major advantage of this approach is the fact that consistent albedo modification rules can be written down immediately.
The CA is constructed as follows: the plane is replaced by a quadratic lattice
![]() , where
, where ![]() , and
the basic spatial units
, and
the basic spatial units ![]() ,
, ![]() can be chosen arbitrarily. Time
proceeds in discrete steps
can be chosen arbitrarily. Time
proceeds in discrete steps ![]() , where
, where ![]() and
and
![]() is again an optional unit. Thus any systems variable F becomes
a function
is again an optional unit. Thus any systems variable F becomes
a function ![]() .
.
The occurrence of vegetation in a particular cell ![]() at time
at time ![]() can
be indicated
by a binary coverage map
can
be indicated
by a binary coverage map ![]() .
The albedo dynamics is then determined by the following rules:
.
The albedo dynamics is then determined by the following rules:
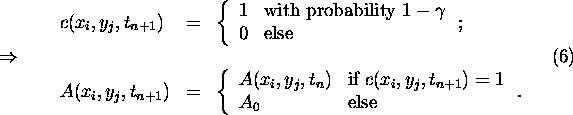
Then choose at random a next-neighbour cell ![]() of
of ![]() and make the following distinction:
and make the following distinction: