Then assume that
where
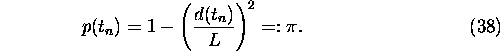
We want finally to demonstrate that the geometry of the remaining growth space is indeed of paramount importance for the ecological performance of our toy biosphere. To this end, we repeat our simulations for a trivial process of habitat reduction, namely progressive shrinking in time of the rectangular core growth area. The prescription for the process is as follows:
Let ![]() denote the size of the lattice, so the cells
denote the size of the lattice, so the cells ![]() of
the system obey the inequalities
of
the system obey the inequalities
![]()
Then assume that
![]()
where ![]() , d(0)=L, and
, d(0)=L, and ![]() for
for ![]() .
That means that the habitable zone is a dwindling central square of approximate
area
.
That means that the habitable zone is a dwindling central square of approximate
area ![]() and is a decreasing function of time
and is a decreasing function of time ![]() . The properties of the so-restricted system can be compared to those
for the above-described patchy one with identical total growth area, i.e. for
. The properties of the so-restricted system can be compared to those
for the above-described patchy one with identical total growth area, i.e. for
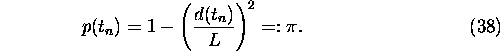
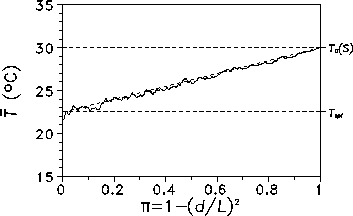
Figure 14: Variation of global mean temperature ![]() with progressive
trivial shrinkage of habitable area. As in Fig. 9, S' has been chosen to
generate
with progressive
trivial shrinkage of habitable area. As in Fig. 9, S' has been chosen to
generate ![]() . The tilted broken line indicates the linear
estimation as expressed in Eq. 39.
. The tilted broken line indicates the linear
estimation as expressed in Eq. 39.
The evolution of the global mean temperature ![]() as a function of
as a function of ![]() under an insolation that corresponds to
under an insolation that corresponds to ![]() is depicted in Fig. 14. Note
that, in contrast to the non-trivially fragmented system, the ``shrinking square
biosphere'' is not capable of planetary homeostatic control:
is depicted in Fig. 14. Note
that, in contrast to the non-trivially fragmented system, the ``shrinking square
biosphere'' is not capable of planetary homeostatic control: ![]() increases almost linearly with growing
increases almost linearly with growing ![]() . This behaviour is approximated
by the formula
. This behaviour is approximated
by the formula
![]()
The markedly different adaptive capabilities induced by habitat geometry
can be explained in a straightforward way. In the first case, where the growth
area is reduced according to the percolation algorithm, we have approximately
![]() non-coverable cells, and almost all of them are adjacent to cells
covered by vegetation. In the second case, where the planetary space decays into
a coverable central square and a non-coverable margin, only a very small number
of ``dead'' cells
non-coverable cells, and almost all of them are adjacent to cells
covered by vegetation. In the second case, where the planetary space decays into
a coverable central square and a non-coverable margin, only a very small number
of ``dead'' cells
![]()
are neighbour on a ``living'' cell. In other words: due to its intricate
patchiness, the surface-to-bulk ratio of a percolation cluster is very large
in comparison with the surface-to-bulk ratio of a simple square covering
the same area!
But the size of the surface is an indicator
for the total heat flow, which can be activated between the sterile and the
fertile zones of Daisyworld. We clearly find that the patchy and lacunary
distribution of living cells over the planet is sufficient to suppress ``hot spots''
via thermal relaxation.