Many of the crucial values for society are being changed under climatic variations more or less smoothly: crop yield, water storage, water level of rivers, sea level etc.. (Note that their ``smoothness'' is determined, in the first place, by their measurability.) Therefore, these values can be considered, generally, as continuous functions of climate change, which is a consequence of the emission of ``greenhouse gases''. This process is determined mainly by the structure and organisation of the world energy system. However, a social perception transforms the continuous range of those values to a discrete set, namely ``good-medium-bad-disaster''. For instance, the difference between a bad crop yield and a catastrophic one may be less than the difference between medium and bad yields, but the social consequences of ``bad'' and ``catastrophic'' yields are not comparable. The impossibility of navigation is a result of the fact that the water levels sink below some critical threshold. A local agricultural disaster may certainly be compensated at the regional scale (with the help of market mechanisms), but there may exist a critical level for total crop production which destroys the market as a whole. For many social systems such critical thresholds (either scalars or vectors or surfaces in the space of basic variables) exist. If a system crosses such boundaries then the system's homeostasis is destroyed.
Therefore, we define a critical event as a crossing of the homeostasis boundary for some social system (see below) after which this system cannot be reconstructed (or will not reconstruct itself).
Note that in numerous works the ``CO![]() -doubling'' is considered as a crucial
point for climate, biota, etc. So, this is not a critical event, and what is
more, the state of the biosphere corresponding to CO
-doubling'' is considered as a crucial
point for climate, biota, etc. So, this is not a critical event, and what is
more, the state of the biosphere corresponding to CO![]() -doubling is not
unique, because it depends substantially on the path of transition from the
present state to the state where CO
-doubling is not
unique, because it depends substantially on the path of transition from the
present state to the state where CO![]() concentration will be doubled. The
concentration of carbon dioxide in the atmosphere is simply one of many
strategic variables of the whole system.
concentration will be doubled. The
concentration of carbon dioxide in the atmosphere is simply one of many
strategic variables of the whole system.
Suppose there is a social system, the state of which is described by the
vector x (in general case x may depend on time, that is, to be a dynamic
variable). We suppose also that the state depends on climate which is described
by the vector ![]() , so that
, so that ![]() .
.
Let ![]() be a homeostasis domain for this system. It is obvious that
the critical level,
be a homeostasis domain for this system. It is obvious that
the critical level, ![]() , is defined by the equation
, is defined by the equation
![]() . In turn, the inequality
. In turn, the inequality ![]() induces the
set
induces the
set ![]() of admissible x with the boundary
of admissible x with the boundary
![]() .
.
Suppose that the inverse mapping ![]() does exist. Then we
can calculate the set
does exist. Then we
can calculate the set ![]() of admissible climates with the
boundary
of admissible climates with the
boundary ![]() , where
, where
![]() .
Note that the mappings
.
Note that the mappings ![]() and
and ![]() may be
non-unique.
may be
non-unique.
The solution of this criticality problem is trivial: if the predicted
climate does not belong to the set ![]() then the state of the
system is catastrophic.
then the state of the
system is catastrophic.
We illustrate these abstract considerations by the following concrete example.
Let our social system be the agriculture system producing cereals. The state of
the system is described only by the crop yield, that is, by the scalar x. If
![]() then we have an ``agricultural disaster'', the value
then we have an ``agricultural disaster'', the value
![]() is determined by economic and social arguments. The
homeostasis domain for this system is defined by the inequality
is determined by economic and social arguments. The
homeostasis domain for this system is defined by the inequality
![]() . Then
. Then ![]() ,
,
![]() (see Fig. 1). If we assume that the
crop yield depends only on the annual temperature
(see Fig. 1). If we assume that the
crop yield depends only on the annual temperature ![]() , then the climate is
described by the scalar
, then the climate is
described by the scalar ![]() and
and ![]() . As a rule, the
dependence is uni-modal, and, how we can see in Fig. 1, the mapping
. As a rule, the
dependence is uni-modal, and, how we can see in Fig. 1, the mapping
![]() is non-unique. Therefore the set
is non-unique. Therefore the set ![]() of
admissible temperatures is the interval
of
admissible temperatures is the interval
![]() with the boundary
with the boundary ![]() .
These two boundary points correspond to two solutions of the equation
.
These two boundary points correspond to two solutions of the equation
![]() .
.
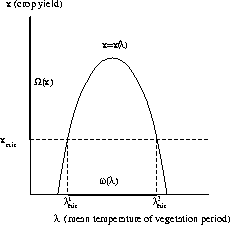
Figure 1: To the definition of the sets ![]() and
and ![]() :
:
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;
![]() .
.
Revenons à nos moutons, we can say that the solution of our criticality problem is trivial if we have:
Let us suppose that there are different deterministic models
![]() and that each of them possesses a different
``predictive power'' depending on its structure, complexity, scientific
uncertainties etc.. The simple way to describe this power is to associate
some specific probability
and that each of them possesses a different
``predictive power'' depending on its structure, complexity, scientific
uncertainties etc.. The simple way to describe this power is to associate
some specific probability ![]() to each predicted value
to each predicted value ![]() . Thus,
some probability measure can be constructed on the basis of the set of models
. Thus,
some probability measure can be constructed on the basis of the set of models
![]() . Another way is to use some stochastic model with a probability
measure. In these cases we can formulate the following probabilistic statement:
the inequality
. Another way is to use some stochastic model with a probability
measure. In these cases we can formulate the following probabilistic statement:
the inequality ![]() takes place for any
takes place for any ![]() with the specific probability
with the specific probability ![]() .
.
Next we have to take into account that there is no ideal prediction for
![]() . Scientific uncertainties in climate prediction will allow us to
predict the value
. Scientific uncertainties in climate prediction will allow us to
predict the value ![]() only with some probability
only with some probability ![]() , so that
instead of unique prediction for
, so that
instead of unique prediction for ![]() we have a set of values for
we have a set of values for
![]() , and each of them can be realised with a specific probability.
Certainly, the suggested method of uncertainty analysis is not unique in a
problem of GW, there are other approaches (see, for instance, [4]),
which can also be used in calculation of corresponding probabilities.
, and each of them can be realised with a specific probability.
Certainly, the suggested method of uncertainty analysis is not unique in a
problem of GW, there are other approaches (see, for instance, [4]),
which can also be used in calculation of corresponding probabilities.
And, finally, for the given ![]() the probability of the event
the probability of the event
![]() is equal to:
is equal to:
![]()
under the normalisation condition
![]()
There is not a problem in generalising this approach to the case when
![]() is a functional and the critical event is also a functional, etc..
is a functional and the critical event is also a functional, etc..
The probability R can be considered as a measure of the risk for the
catastrophic event ![]() . But we also have to keep in mind
the following facts:
. But we also have to keep in mind
the following facts:
Certainly, it is easier said than done (especially this is true for the first two points), but for relatively simple systems it is possible. We have shown above how to do this, for instance, for such a system as an agricultural one.