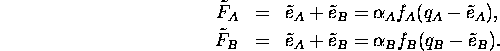
Thus, we have proved that the solution of system
(5) describes the equilibrium. The equilibrium is
stable. Indeed, if, for instance, the actor A chooses the
emission ![]() , which differs from the equilibrium value
, which differs from the equilibrium value ![]() ,
then the value of his utility function
,
then the value of his utility function ![]() will be
higher than the value of this function in the equilibrium.
The stability is a very important argument in the process
of selection among different virtual decision makings.
This principle (stability) guarantees the ``fair play''
since none of the actors has an advantage to depart from the
accepted agreement (equilibrium).
will be
higher than the value of this function in the equilibrium.
The stability is a very important argument in the process
of selection among different virtual decision makings.
This principle (stability) guarantees the ``fair play''
since none of the actors has an advantage to depart from the
accepted agreement (equilibrium).
Nevertheless, one problem appears: is the suggested
choice efficient? In other words, would there be another choice,
which is more advantageous for both actors than the
equilibrium one? It is proved that the equilibrium
solution is efficient, i.e., it can not be improved for
both actors simultaneously, and the solution belongs to
the Pareto's set. If we would prove that decreasing, for
instance, ![]() , we necessarily increase
, we necessarily increase ![]() , then by the same
token the main statement is proved.
, then by the same
token the main statement is proved.
Let ![]() and
and ![]() satisfy the conditions (4), hence, they
are the solution of (5). Let us try to decrease the
value
satisfy the conditions (4), hence, they
are the solution of (5). Let us try to decrease the
value ![]() changing only
changing only ![]() . Since in
the equilibrium
. Since in
the equilibrium ![]() then by increasing
then by increasing ![]() we
get
we
get ![]() , and
, and ![]() increases. On the contrary, if we
decrease
increases. On the contrary, if we
decrease ![]() then
then ![]() , and
, and ![]() increases also.
We can decrease
increases also.
We can decrease ![]() only if we decrease
only if we decrease ![]() , but this
implies an increase of
, but this
implies an increase of ![]() . Therefore, the equilibrium
solution is efficient and the point
. Therefore, the equilibrium
solution is efficient and the point ![]() belongs to
the Pareto's set.
belongs to
the Pareto's set.
Note that all these results come from a partial
application of the general theory mentioned in [4].
Speaking about an application of the game theory to the
problem of CO![]() emissions and their reductions we must say
a few words about other approaches.
emissions and their reductions we must say
a few words about other approaches.