The problem is how to distribute the global
reduction of CO
emission to individual reductions. A
solution can be found if we apply a game theoretic
concept to this problem: different countries are
actors in a game with non-antagonistic interests (either
in Germeier's sense [1] or in a more traditional sense [2]).
It seems to us that the ``game'' approach would be very
natural in application to the problem.
Let us consider the simplest example: there are two
independent actors, A and B (two countries or regions),
each of them releases 
and 
amounts of CO per year (in carbon units) into the atmosphere. The total
emission is equal to 
. As a rule, these emissions
are connected to the energy sector of their economies. We
used the term ``independent actors'' keeping in mind that
each actor establishes an own level of emission taking
into account only an own interest. There are no
hierarchical connections between them, but other informal
connections may be, in particular, the tendency to avoid
hardly evaluable consequences of climate change. Since
the climate change is determined, in turn, by the
concentration of CO in the atmosphere, then (if we
suppose implicitly that a new climatic equilibrium is
stabilised very quickly) the climate change will depend
on the total emissions q. The best strategy is to save
status quo, or, at least, to be as close as possible to
this state.
Note that another game theory approach is possible [3].The approach is based on the fact that the countries differ in their vulnerability to global warming (GW) and that two coalitions (suffering and not suffering countries are included) will possibly be formed. The problem is modelled as an economic infinite-horizon differential game. The player negotiate an agreement among Pareto’s efficient programs.
Returning to our problem we understand that in order to
realise this strategy we must reduce the total emissions
down to zero, but it is unrealistic. It is supposed that
the emissions were reduced from to 
and to 
(
; 
), the total emissions were reduced
from q to e, where 
. There is a common
``altruistic'' interest: 
. This aim is very implicit
and badly perceived by a concrete actor. He perceives
only that it would be better to avoid a global disaster and for
this it is necessary to reduce the total emission. For this
reason we call such a strategy an ``altruistic'' one. On
the other hand, the reduction of emission requires
certain additional expenditures. It is natural to suppose
that these expenditures are described by the functions
and 
which are monotonously decreasing
functions of their arguments. Each actor will tend to
minimise his own losses resulting from the reduction
of his own emissions, i.e., he has an ``egoistic''
interest: 
, 
. And finally, we get:
Thus, each actor is in a situation when he has to choose
the value of reduction in such a way that would satisfy the
both criteria. For this, some problem of multicriteria
optimisation must be solved, and, in turn, we need an
additional hypothesis making the utility
functions of the actors commensurable. We shall weigh ``egoistic'' and
``altruistic'' criteria for each actor introducing
coefficients 
and 
, so-called ``coefficients of
egoism''. This coefficient is very large, if the actor
uses a very egoistic strategy, and vice versa, if the
actor is a ``super-altruist'' then the corresponding
coefficient is very small. Using these coefficients we
can fold the criteria (1) into one criterion for each
actor:
In other words, each actor considers the maximal from two
values, 
and e or 
and e, as an evaluation of his
state. The aim of the actor A is the choice of such an
emission that 
. However, the value of 
depends not only on but also on , i.e. on the choice
of the second actor. The analogous situation takes place
also for the second actor. This is a typical conflict
situation as far as the actors tend to different aims:
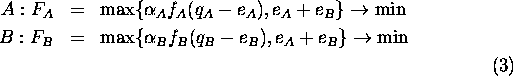
How to resolve this?