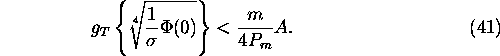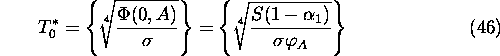Next: About the numerical estimation
Up: Parametrization
Previous: Equilibrium as a function
This equilibrium is the equilibrium of the ``naked'' planet. Let us consider it in
detail.
If 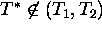 , i.e. the equilibrium temperature lies outside
the tolerance interval for photosynthesis, then this equilibrium is always
stable. If
, i.e. the equilibrium temperature lies outside
the tolerance interval for photosynthesis, then this equilibrium is always
stable. If 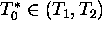 then the equilibrium is stable, if
then the equilibrium is stable, if
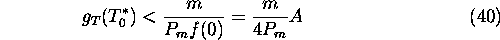
or
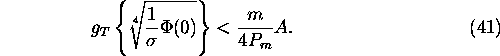
Suppose the reciprocal operator 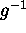 exists, so
that
exists, so
that
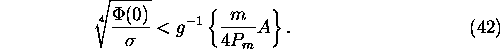
Since
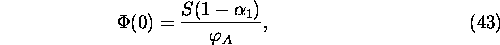
then the left part of (42) depends only on the characteristics and total
amount of carbon in the system. The right part of (42) depends only
on the biotic characteristics of the planetary vegetation and also the total
carbon. If we assume that the equilibrium temperature for the ``naked'' planet is
fixed -- the total carbon is fixed also -- but we can change (e.g. in an evolutionary
way) the vegetation characteristics, then we can pass from a stable ``naked''
equilibrium to an unstable one.
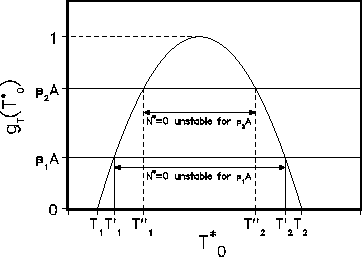
Figure 9: To the problem of stability for "naked" equilibrium: in the interval 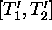 with
with 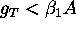 it is unstable (
it is unstable (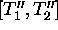 for
for 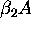 ). For
). For
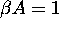 this interval is reduced to a point, above 1 the equilibrium
is stable for any T.
this interval is reduced to a point, above 1 the equilibrium
is stable for any T.
Let us consider Fig. 9: from this picture we can see that the condition
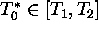 , i.e. the condition that the equilibrium temperature
belongs to the photosynthesis tolerance interval, is not sufficient in order to pass
to the instability of a ``naked'' equilibrium, i.e. for the ``origin of life'' It
is necessary that the temperature
, i.e. the condition that the equilibrium temperature
belongs to the photosynthesis tolerance interval, is not sufficient in order to pass
to the instability of a ``naked'' equilibrium, i.e. for the ``origin of life'' It
is necessary that the temperature 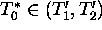 , then the ``naked''
equilibrium becomes unstable and ``life'' can occur. This interval depends
on such biotic characteristics as the residence time of carbon in the biota
(
, then the ``naked''
equilibrium becomes unstable and ``life'' can occur. This interval depends
on such biotic characteristics as the residence time of carbon in the biota
(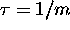 ) and its maximum productivity
) and its maximum productivity 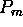 . We call the interval
. We call the interval
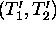 the ``vegetation tolerance interval''
the ``vegetation tolerance interval''
Let us consider the change of the product 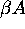 . Its increase, which
corresponds
either to the decrease of carbon residence time in the biota or to a decrease of the
maximal productivity of photosynthesis, leads to a reduction of the vegetation
interval. And, vice versa, the decrease of
. Its increase, which
corresponds
either to the decrease of carbon residence time in the biota or to a decrease of the
maximal productivity of photosynthesis, leads to a reduction of the vegetation
interval. And, vice versa, the decrease of 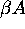 , because of the increase of
residence time or increase of maximal productivity, increases the vegetation interval.
, because of the increase of
residence time or increase of maximal productivity, increases the vegetation interval.
It is obvious that if 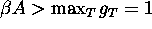 , then the ``naked'' equilibrium
is stable for any
, then the ``naked'' equilibrium
is stable for any 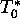 , and ``life'' cannot arise in the vicinity
of this equilibrium. In other words, there is some critical combination from
, and ``life'' cannot arise in the vicinity
of this equilibrium. In other words, there is some critical combination from
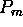 , m (or
, m (or 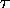 ), and A:
), and A:

or

On the other hand
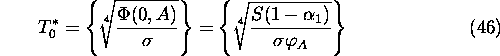
is the monotonous increasing function of A, since 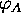 monotonously
decreases with the growth of A. Since
monotonously
decreases with the growth of A. Since
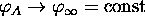 ,
then
,
then 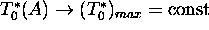 , if
, if
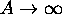 .
.
In fact there are two bifurcation parameters: 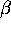 and A. Note that
and A. Note that
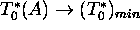 , if
, if 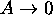 , where
, where
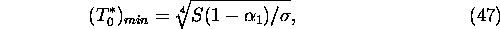
since 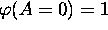 .
.
Let us assume that 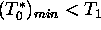 , and
, and 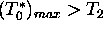 , then
we have the stability diagram as in Fig. 10. The border in the
, then
we have the stability diagram as in Fig. 10. The border in the 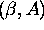 domain is determined by
the function
domain is determined by
the function
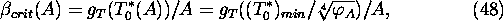
whereat for 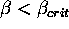 the ``naked'' equilibrium is unstable.
the ``naked'' equilibrium is unstable.
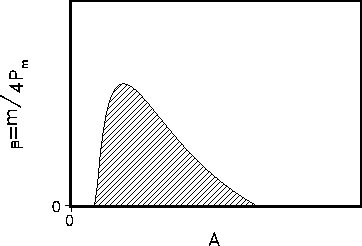
Figure 10: Stability border for 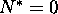 in the
in the 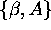 domain:
domain: 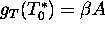 ,
, 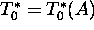 . The shaded area indicates the area of instability of
. The shaded area indicates the area of instability of
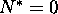 where ``life'' can arise in the vicinity of the ``naked'' equilibrium.
where ``life'' can arise in the vicinity of the ``naked'' equilibrium.



Next: About the numerical estimation
Up: Parametrization
Previous: Equilibrium as a function
Werner von Bloh (Data & Computation)
Thu Jul 13 11:24:58 MEST 2000