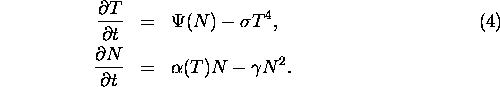
Further we can see that the most important properties of the general problem can be reduced from analysis of the system (4).
First we will consider solutions, which do not depend on the
spatial coordinate x. These solutions correspond to the so-called ``uniform
biosphere'', i.e. the biosphere with characteristics which are identical for
any point of the planet. The evolution in time of the uniform biosphere derived from eqs. 2 and 3 is
determined by the following nonlinear system:
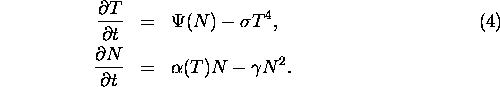
Further we can see that the most important properties of the general problem can be
reduced from analysis of the system (4).
Let us consider the equilibrium points ![]() ,
, ![]() .of eq. 4.
Then
they must satisfy the equations:
.of eq. 4.
Then
they must satisfy the equations:
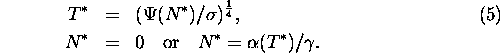
It is better to consider them graphically on the plane ![]() . Depending
on the value
. Depending
on the value ![]() 6 cases can be differentiated in respect to the number
and position of the intersections between curve (I):
6 cases can be differentiated in respect to the number
and position of the intersections between curve (I):![]() and
(II):
and
(II):![]() (see Fig. 4a-f). These intersections
fulfil eq. (5) and are equilibria of (4).
(see Fig. 4a-f). These intersections
fulfil eq. (5) and are equilibria of (4).
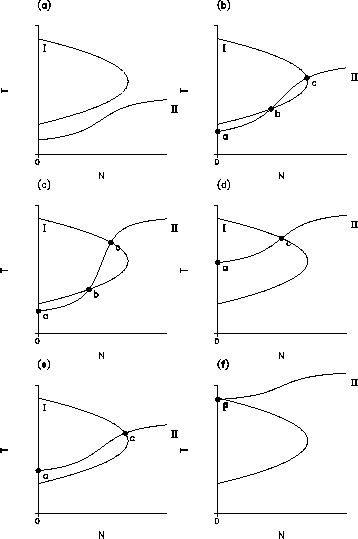
Figure 4: Graphical representation of (5) at different ![]() .I:
.I:![]() ,
II:T=
,
II:T=![]() . The different stationary points
. The different stationary points ![]() are
denoted by letters a-c.
are
denoted by letters a-c.
Up to three equilibria denoted as ![]() ,
,
![]() , and
, and ![]() can be found.
The points a in Fig. 4a-f are
semi-trivial equilibria, where
can be found.
The points a in Fig. 4a-f are
semi-trivial equilibria, where
![]()
If ![]() then we can speak about our planet as the ``cold desert'', if
then we can speak about our planet as the ``cold desert'', if
![]() then about the ``hot desert''.
then about the ``hot desert''.
Let us calculate the eigenvalues ![]() of the Jacobi matrix
of the Jacobi matrix
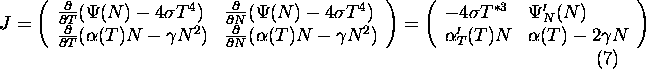
for (4):
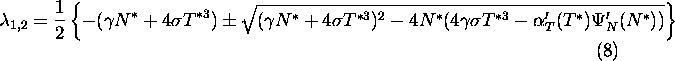
The value of the ![]() characterizes the behaviour of the system in the
vicinity of the equilibria
characterizes the behaviour of the system in the
vicinity of the equilibria ![]() :
:
For the ``semi-trivial'' points with ![]() we have
we have
![]()
and if either ![]() or
or ![]() the equilibrium
the equilibrium ![]() is a stable node (
is a stable node (![]() ), if
), if ![]() then the equilibrium
is a saddle point (
then the equilibrium
is a saddle point (![]() ).
).
For the ``non-trivial'' equilibrium with ![]() we have the following:
we have the following:
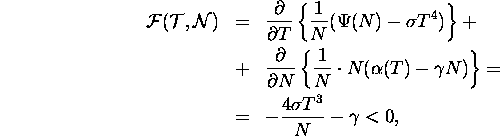
The structure of phase plane for the system (4) is sufficiently simple.
Let us come back to the Figs. 4a-f: Now phase portraits of system (4) are plotted for parameters equivalent to the corresponding Figs. 4 in respect to the number and positions of the equilibria. Their stability is analyzed in the following.
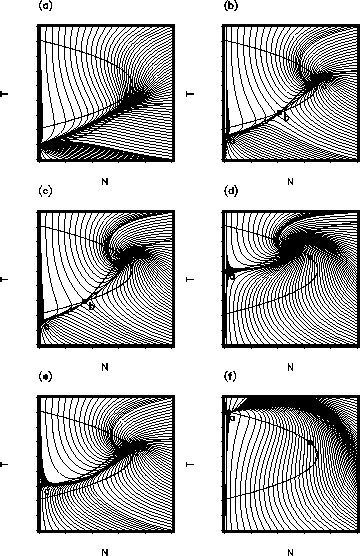
Figure 5: Phase portrait of system (4) corresponding to Figs. 4.
In Fig. 5a the point a is a stable node, the final state of this planet (for any initial
conditions) is the ``cold desert'' (![]() , i.e. no vegetation can occur). It exists always if
, i.e. no vegetation can occur). It exists always if
![]()
If ![]() as before, but
as before, but ![]() ,
we have the following picture (Fig. 5b):
In this case the point a is a stable node, the point b is a saddle and the point
c is a stable node, since
,
we have the following picture (Fig. 5b):
In this case the point a is a stable node, the point b is a saddle and the point
c is a stable node, since ![]() .
.
It is interesting that there are two stable final states (point a and c), and
the singular trajectory of saddle point b divides the quadrant N>0,T>0 into
two domains of attractivity. The initial condition of temperature and amount of vegetation determines whether vegetation can exist or not.
Let ![]() (Fig. 5c), and, in addition, the inequality (10) is valid (note if
(Fig. 5c), and, in addition, the inequality (10) is valid (note if
![]() this inequality is not valid), then the point c is a stable
focus. As before, the point a is a stable node, the point b is a saddle.
If
this inequality is not valid), then the point c is a stable
focus. As before, the point a is a stable node, the point b is a saddle.
If ![]() the phase picture (Fig. 5d,e) changes: The point a becomes a saddle
point, the point c is, as before, either a stable node or a stable focus.
In Fig. 5f the point a is a stable node that corresponds to the ``hot desert''
(
the phase picture (Fig. 5d,e) changes: The point a becomes a saddle
point, the point c is, as before, either a stable node or a stable focus.
In Fig. 5f the point a is a stable node that corresponds to the ``hot desert''
(![]() ).
).