The role of weathering for the Earth`s climate was first described by Walker et al.[7]. In
particular,
the potential of weathering to stabilize the Earth's surface temperature by a negative feedback
mechanism that is strongly modulated by the biosphere has gained recent
interest (see, e.g., [6, 8, 9]).
Compared to subareal
weathering, silicate-rock weathering on land primarily controls long-term atmospheric
CO
content [10]. The question of to what extent
the biota are actually able to play an active role in stimulating the strength of the main carbon
sink through weathering is crucial for an understanding of the dynamic properties of the
overall Earth system.
The total process of weathering embraces first the reaction of silicate minerals with
carbon dioxide,
second the transport of weathering products, and third the deposition of
carbonate minerals in
sediments. The availability of cations plays the main role in these processes and is the limiting
factor in the carbonate-sediments-forming reaction (third process) between cations
(Ca
and
Mg) and carbonate anions (CO
). Therefore, for the mathematical
formulation we have only
to take into consideration the amount of released cations and their runoff (first and second
process), respectively.
Following Walker et al.[7], the weathering rate 
, as a global average
value,
is the product of cations concentration
in water (in mass per unit volume) and runoff (in volume per unit area per unit time).
Therefore, the weathering rate is the mass of cations formed per unit area and unit time.
Combining
the direct temperature effect on the weathering reaction, the weak temperature effect on river
runoff, and the dependence of weathering on soil CO concentration
[7, 1], the global mean silicate-rock weathering rate can be formulated via the
following implicit equation:
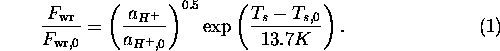
Here the pre-factor outlines the role of the CO concentration in the soil,
; 
is
the activity of 
in fresh soil-water and depends on and the global
mean surface temperature 
. The quantities
, 
, and 
are the present-day
values for the weathering rate, the activity, and the surface temperature, respectively.
The activity
is itself a function of the temperature and the CO concentration in the soil.
The equilibrium constants for the chemical activities of the carbon and sulfur systems involved
have been taken from Stumm and Morgan[12].
Note that the sulfur content in the soil also contributes to the
global weathering rate, but its influence does not depend on temperature. It can be regarded as
an overall weathering bias, which has to be taken into account for the estimation of the
present-day value.
Eq. 1 is the key relation for our models. For any given weathering
rate the surface temperature and the CO concentration in the soil can be calculated
self-consistently, as will be shown below. can be assumed to be linearly
related to
the terrestrial biological productivity 
(see [13]) and the atmospheric
CO
concentration
. Thus we have
where 
, 
and 
are again present-day
values. Biologically enhanced Hadean and Archaean weathering processes would have been very
different from the modern ones, although the purely inorganic processes are the same. Nevertheless, in our
calculations we assume that at least as far back to the Proterozoic, the biosphere generates the same effects
as today, namely the enhancement of CO concentration in soil compared to the
atmospheric value.
Besides the biotic influence, which will be discussed later, the Earth`s surface temperature
plays a
dominant role in influencing the intensity of weathering as a massive carbon sink, as explained
above. Caldeira and Kasting[1] have introduced the following simplified climate
model for calculating : The time dependence of the solar luminosity I(t)
is fitted for the interval 
by the function
The energy balance between incoming and outgoing radiation is given by
where a is the planetary albedo, 
is the Stefan-Boltzmann constant, and
is the effective black-body radiation temperature which has to be increased by the greenhouse
warming
as function of the atmospheric carbon dioxide value . For an
explicit
formulation of the logarithmic dependence, see Caldeira and Kasting[1].
Then the global surface temperature is given by the following implicit equation
This greenhouse model is valid for a very broad range of temperatures and CO partial
pressures
and 
).
Nevertheless, if we wish to investigate the very early terrestrial atmosphere at about 4 Ga
ago
that is believed to have had a between 
and 
ppm
[14],
an extended greenhouse model working within a larger range of even higher CO partial
pressures
is necessary. Such an improved greenhouse model is presented for example by
Williams[15].
The main role of the biosphere in the context of our model is to increase
in relation to the atmospheric CO partial pressure
and proportional to the biologic productivity
. is itself a function of various parameters such as water supply, photosynthetic
active radiation
(PHAR), nutrients (e.g., N, P and C), , and .
In the framework of our Earth system model the biological productivity is considered to
be a function of
temperature and CO partial pressure in the atmosphere only. According to Liebig's
principle, can be cast into
a multiplicative form, i.e.
The maximum productivity, 
, is estimated to be twice the present value
[13], thus
.
Following Volk[13], Michaelis-Menten hyberbolas (see, e.g.,[16])
are suitable
for describing the
functional behaviour of 
:
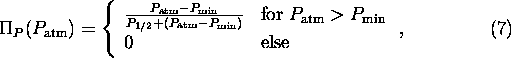
where 
is the value at which 
, and
ppm.
Eq. 7 evidently tends to 1 for 
. Experiments of
plant growth under
increased have shown an upper tolerance limit with respect to
[17].
Therefore, following Kump and Volk[18], we investigate a second class of Earth system
models with a parabolic
relation of the
CO dependent growth function in analogy to the Daisyworld models of
Watson and Lovelock[19] (see also:[20]):
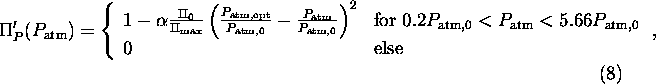
where 
is the optimum
CO partial pressure for
photosynthesis, 
.
The temperature dependence of 
is described by a parabolic function used already
by Caldeira and Kasting[1]. It has a maximum at 
:
The resulting function 
is in any case a good description of the
so-called
net primary productivity (NPP) for the present biosphere. Let us emphasize that we do not
consider
the role of the carbon storage pool of biosphere in this paper. Within our approach, the
biosphere productivity provides a measure
for the biotic pump increasing with respect to the abiotic diffusive
equilibrium between and .
As a consequence, we need not take into account the net productivity containing both the
production and the
decomposition of biomass. On the other hand, it is still unclear whether the ansatz for
is strictly valid for the Archaean and Proterozoic
eras when biomass was produced by primitive organisms like algo-bacterial mats.
Our Eq. 9 can be extended to temperatures even higher than 
in
order to incorporate
hyperthermophiles [21]. Nevertheless, in order
to facilitate comparability of our results with those found by Caldeira and Kasting[1],
we will use the temperature-dependent term given in Eq. 9.