Atmosphere Model Aeolus 2.0

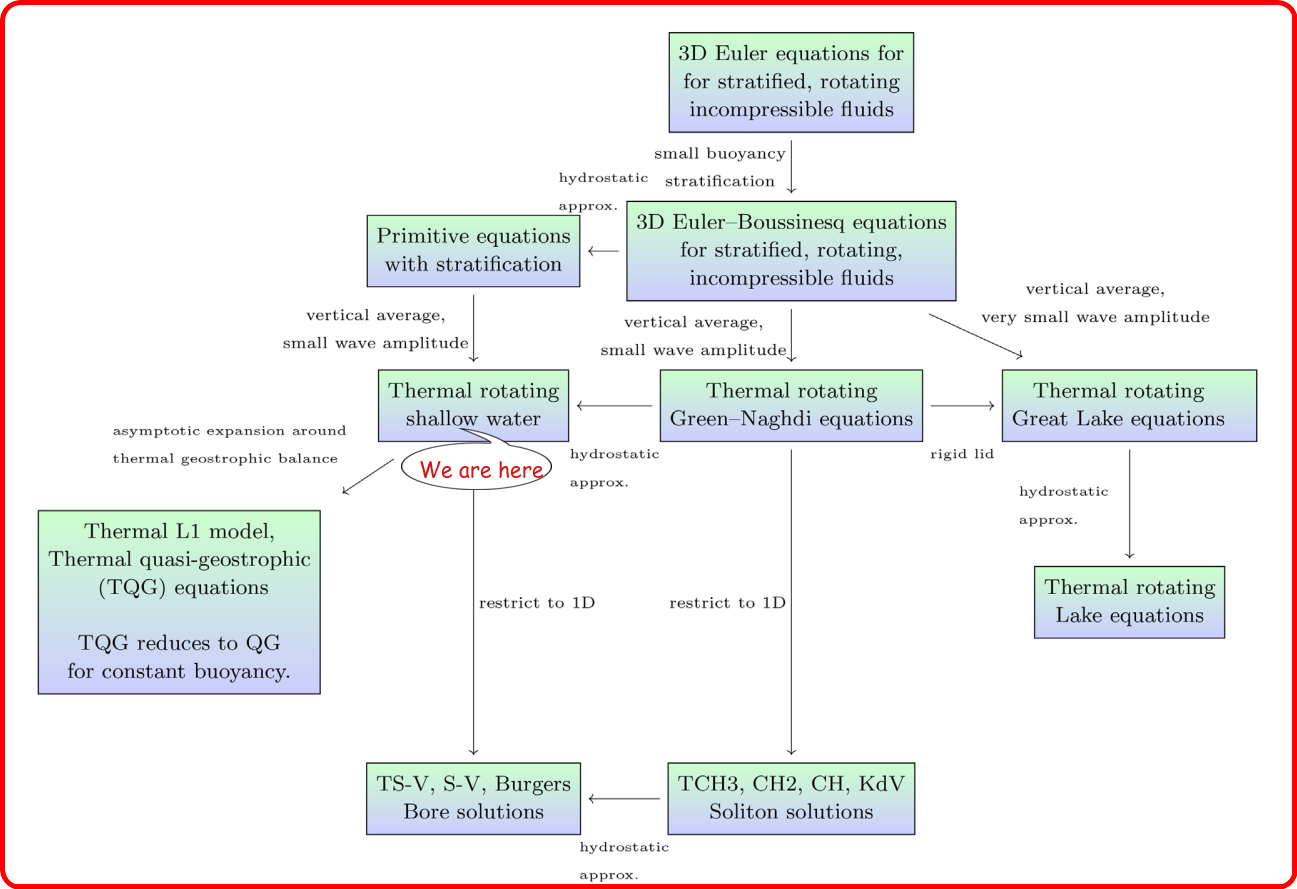
Model Description

Aeolus 2.0 is an in-house open-source numerical model designed to simulate atmospheric circulations. The model's dynamical core is based on a multi-layer pseudo-spectral moist-convective Thermal Rotating Shallow Water (mcTRSW) model. The Dedalus algorithm, renowned for its handling of spin-weighted spherical harmonics, manages the pseudo-spectral problem-solving tasks. One advantage of spin-weighted spherical harmonics is that differentiation on the sphere remains regular everywhere. In the classical setup of shallow-water models, the fluid is homogeneous, incompressible, and under hydrostatic balance. Therefore, gradients of mean temperature and density are invariant in this setup. However, the TRSW model employs inhomogeneous layers, allowing horizontal variations in potential temperature.  The elucidation of the multi-layer Thermal Rotating Shallow Water (TRSW) model and its associated moist convection, characterized by minimal parameterization across the entire spherical domain, has been comprehensively detailed in the publication by Rostami et al., 2022.

The model captures the temporal and spatial evolution of vertically integrated potential temperature, pressure, water vapor, precipitation, and the intricate influence of bottom topography. It comprehensively characterizes velocity fields in both the lower and upper troposphere, employing resolutions spanning a spectrum from smooth to coarse. This enables the exploration of a wide range of dynamic phenomena with varying levels of complexity.

Layer versus Level Models

Aeolus 2.0 is characterized by its use of a layer model, a key feature that distinguishes it from level models commonly employed in geophysical fluid dynamics. Both approaches are used to represent the vertical structure of the atmosphere and oceans, but they differ in how they handle stratification. While level models are able to incorporate thermodynamics more straightforwardly, they tend to be less accurate, particularly at higher vertical modes. This discrepancy arises from the way each model represents the density profile: level models assume a continuously stratified density and use finite differencing at fixed depths. In contrast, layer models approximate the continuous density profile with discrete layers, where the depth of the interfaces can change over space and time. The limitations of finite differencing in level models become apparent at small scales, leading to accuracy issues. Layer models avoid these problems because their piecewise constant density profile is physically valid, and the equations of motion are tailored to this specific form of stratification. A clear example of the difference between these two models can be seen in the Laplace tidal equations, which describe tidal behavior in the ocean and atmosphere. These equations function as a one-layer model, with no direct equivalent in the level model framework.

Spin-Weighted Spherical Harmonics

In the numerical methodology employed in Aeolus 2.0, the Dedalus algorithm is utilized. The Dedalus algorithm incorporates the use of spin-weighted spherical harmonics, as documented in the works of Vasil et al. (2019)  and Lecoanet et al. (2019). Spin-weighted spherical harmonics were originally introduced by Gelfand and Shapiro (1956) in their studies related to the Lorenz group. One key advantage of utilizing spin-weighted spherical harmonics in combination with spinor basis vectors is the ability to perform differentiation operations on the spherical domain in a manner akin to Fourier series operations. This property enables regular and well-behaved diagonal wavenumber multiplication across the entire sphere, eliminating the necessity for traditional singular gradients at the poles. This advantageous feature enhances the numerical stability and accuracy of calculations performed within the mcTRSW dynamical core on a spherical domain.

References